STATISTICAL QUALITY CONTROL

Basic Concepts

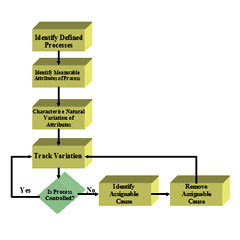
• Statistical Quality Control or Statistical Process Control (SPC) is an effective method of monitoring a process through the use of control charts.
• Control charts enable the use of objective criteria for distinguishing background variation from events of significance based on statistical techniques.Much of its power lies in the ability to monitor both process center and its variation about that center.
• By collecting data from samples at various points within the process, variations in the process that may affect the quality of the end product or service can be detected and corrected, thus reducing waste as well as the likelihood that problems will be passed on to the customer.
• its emphasis on early detection and prevention of problems, SPC has a distinct advantage over quality methods, such as inspection, that apply resources to detecting and correcting problems in the end product or service.
• In addition to reducing waste, SPC can lead to a reduction in the time required to produce the product or service from end to end. This is partially due to a diminished likelihood that the final product will have to be reworked, but it may also result from using SPC data to identify bottlenecks, wait times, and other sources of delays within the process.
• Process cycle time reductions coupled with improvements in yield have made SPC a valuable tool from both a cost reduction and a customer satisfaction standpoint.

Statistical Process Control was pioneered by Walter A. Shewhart in the early 1920s. W. Edwards Deming later applied SPC methods in the United States during World War II, thereby successfully improving quality in the manufacture of munitions and other strategically important products. Deming was also instrumental in introducing SPC methods to Japanese industry after the war had ended.

Shewhart created the basis for the control chart and the concept of a state of statistical control by carefully designed experiments. While Dr. Shewhart drew from pure mathematical statistical theories, he understood that data from physical processes seldom produces a "normal distribution curve" (a Gaussian distribution, also commonly referred to as a "bell curve"). He discovered that observed variation in manufacturing data did not always behave the same way as data in nature (for example, Brownian motion of particles). Dr. Shewhart concluded that while every process displays variation, some processes display controlled variation that is natural to the process (common causes of variation), while others display uncontrolled variation that is not present in the process causal system at all times (special causes of variation).

Process Control

Process control is a statistics and engineering discipline that deals with architectures, mechanisms, and algorithms for controlling the output of a specific process.

For example, heating up the temperature in a room is a process that has the specific, desired outcome to reach and maintain a defined temperature (e.g. 20°C), kept constant over time. Here, the temperature is the controlled variable. At the same time, it is the input variable since it is measured by a thermometer and used to decide whether to heat or not to heat. The desired temperature (20°C) is the set point. The state of the heater (e.g. the setting of the valve allowing hot water to flow through it) is called the manipulated variable since it is subject to control actions.

A commonly used control device called a programmable logic controller, or a PLC is used to read a set of digital and analog inputs, apply a set of logic statements, and generate a set of analog and digital outputs. Using the example in the previous paragraph, the room temperature would be an input to the PLC. The logical statements would compare the set point to the input temperature and determine whether more or less heating was necessary to keep the temperature constant. A PLC output would then either open or close the hot water valve, an incremental amount, depending on whether more or less hot water was needed. Larger more complex systems can be controlled by a Distributed Control System (DCS) or SCADA system.

In practice, process control systems can be characterized as one or more of the following forms:

• Discrete – Found in many manufacturing, motion and packaging applications. Robotic assembly, such as that found in automotive production, can be characterized as discrete process control. Most discrete manufacturing involves the production of discrete pieces of product, such as metal stamping.

• Batch – Some applications require that specific quantities of raw materials be combined in specific ways for particular durations to produce an intermediate or end result. One example is the production of adhesives and glues, which normally require the mixing of raw materials in a heated vessel for a period of time to form a quantity of end product. Other important examples are the production of food, beverages and medicine. Batch processes are generally used to produce a relatively low to intermediate quantity of product per year (a few pounds to millions of pounds).

• Continuous – Often, a physical system is represented though variables those are smooth and uninterrupted in time. The control of the water temperature in a heating jacket, for example, is an example of continuous process control. Some important continuous processes are the production of fuels, chemicals and plastics. Continuous processes, in manufacturing, are used to produce very large quantities of product per year (millions to billions of pounds).

Applications having elements of discrete, batch and continuous process control are often called hybrid applications.